Machine d'Atwood et treuil - [S'informer et apprendre en ligne]

Dynamique du solide rigide

Machine d’Atwood et treuil

Moment d’inertie et masse linéique

Expression de l’accélération angulaire de la poulie de la machine d’Atwood lorsqu’on tient compte de sa masse et de la masse du fil.

Article mis en ligne le 15 janvier 2007

dernière modification le 18 mai 2015

par Bernard Vuilleumier

L’étude de la machine d’Atwood néglige en général la masse du fil qui relie les deux objets, voire parfois même le moment d’inertie de la poulie. Nous établissons ici l’expression de l’accélération angulaire de la poulie en tenant compte de son moment d’inertie et de la masse du fil. Nous montrons que cette expression permet de retrouver les accélérations angulaires obtenues lorsqu’on néglige la masse du fil et/ou la masse de la pièce en rotation.

Atwood’s Machine with Rotational Inertia from the Wolfram Demonstrations Project by Aaron King

Deux objets de masse et , avec > , sont attachés aux extrémités d’un câble de masse linéique $\mu$ . Celui-ci est enroulé sur un cylindre plein de rayon et dont la masse totale (câble enroulé compris) vaut $m_{tot}.$ Initialement, les deux objets sont immobiles. Le point d’attache de est à une distance verticale de l’axe de rotation et celui de à une distance , avec < On livre le système à lui-même.

**Variante de la machine d’Atwood**

Dans ce dispositif, on ne néglige ni la masse du câble qui relie les deux objets ni celle du cylindre sur lequel il est enroulé.

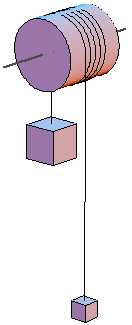
Donnez l’expression littérale de l’accélération angulaire $\alpha$ du cylindre en fonction des quantités connues , , $m_{tot}$ , $\mu$ , , et dans les trois cas suivants :

a) on néglige la masse du câble et la masse du cylindre ;
b) on néglige la masse du câble ;
c) on tient compte de la masse du câble et du cylindre.

Expression des différentes accélérations angulaires

a) En négligeant la masse du câble et celle du cylindre, le problème peut se
traiter ainsi. Nous examinons les forces qui agissent sur chaque objet séparément et nous appliquons, à chacun d’eux, la relation fondamentale de la dynamique :

$\Sigma \vec F=m\vec a$

Nous obtenons, en composantes selon un axe orienté vers le haut (on choisit arbitrairement de compter positivement les forces et les accélérations orientées vers le haut), pour l’objet 1 :

et pour l’objet 2 :

L’accélération de l’objet 1 est dirigée vers le bas (signe -) et celle de l’objet 2 vers le haut (signe +). Ces deux accélérations ont la même grandeur. Si la masse du cylindre est négligée, les tensions et ont également la même grandeur. Posons dans les deux égalités ci-dessus et soustrayons la première à la deuxième. Nous obtenons :

En isolant et en divisant par nous obtenons l’accélération angulaire $\alpha=\frac{a}{r} :$

$\alpha=\frac{m_1-m_2}{(m_1+m_2)r}g$

b) Lorsqu’on néglige la masse du câble et qu’on tient compte de celle du cylindre, il est possible d’utiliser la relation fondamentale de la dynamique appliquée aux solides rigides (la somme des moments de force qui agissent sur le cylindre est égale au produit du moment d’inertie du cylindre par accélération angulaire du cylindre) :

$\Sigma M=I\alpha$

Les deux moments de forces sont ceux de et de

Le moment de force exercé par le brin gauche du câble produit une rotation dans le sens trigonométrique positif (signe +) et le moment de force exercé par le brin droit du câble produit une rotation dans le sens trigonométrique négatif (signe -). Si la masse du cylindre n’est pas négligeable, les tensions et n’ont pas la même grandeur et la relation fondamentale de la dynamique appliquée aux solides rigides permet d’écrire :

$r(T_1-T_2)=I\alpha$

Nous pouvons exprimer les tensions en considérant les forces qui agissent sur chaque objet séparément et en appliquant la relation fondamentale de la dynamique à chacun d’eux :

$T_1-m_1 g=-m_1 \alpha r$ $T_2-m_2 g=m_2 \alpha r$

Nous avons exprimé l’accélération de chaque objet à l’aide de l’accélération angulaire $a = \alpha r.$ En éliminant les tensions et entre les trois équations précédentes et en résolvant par rapport à $\alpha$ , nous obtenons l’accélération angulaire du cylindre :

$\alpha=\frac{(m_1-m_2)r}{I+(m_1+m_2)r^2}g$

Cette accélération angulaire $\alpha$ fait intervenir le moment d’inertie du cylindre. S’il est nul, nous retrouvons bien l’accélération angulaire obtenue sous le point a).

c) Si nous tenons compte de la masse du câble le poids des brins qui supportent les objets modifient les tensions et qui s’obtiennent à partir des équations suivantes :

$T_1-(m_1+\mu d_1) g=-(m_1+\mu d_1) \alpha r$ $T_2-(m_2+\mu d_2) g=(m_2+\mu d_2) \alpha r$

En éliminant les tensions et comme dans le point b) ci-dessus et en résolvant par rapport à $\alpha$ nous obtenons l’accélération angulaire cherchée :

$\alpha=\frac{(m_1-m_2+(d_1-d_2)\mu)r}{I+(m_1+m_2+(d_1+d_2)\mu)r^2}g$

Cette accélération fait intervenir le moment d’inertie du cylindre et la masse linéique $\mu$ du câble. Elle dépend en outre des longueurs de câble et qui sont des fonctions de l’angle $\theta$ dont le cylindre a tourné. Elle permet de retrouver les accélérations obtenues sous a) et b) en annulant respectivement :

a) le moment d’inertie du cylindre et la masse linéique $\mu$ du câble
b) la masse linéique $\mu$ du câble.

Conclusion

La dernière expression de l’accélération angulaire, qui tient compte de la masse de la poulie et de celle du câble, est la plus générale : elle permet de retrouver les expressions de l’accélération lorsqu’on néglige la masse du câble, la masse de la poulie ou la masse des deux.

Exercices

Questions - réponses

Dans la même rubrique